這是”四輪車驅動控制”系列,分多個小節來介紹:
1. 八.四輪車驅動開發之一:正/逆向運動學分析
2. 九.四輪車驅動開發之二: 配置PWM驅動直流電機
3. 十.四輪車驅動開發之三: 巧用編碼器獲取電機轉速信息
4. 十一.四輪車驅動開發之四: 理解直流電機PID控制器
5. 十二.四輪車驅動開發之五: 由淺至深理解6軸陀螺儀姿態解算算法(上)
? ? 十三.四輪車驅動開發之五: 由淺至深理解6軸陀螺儀姿態解算算法(中)
? ? 十四.四輪車驅動開發之五: 由淺至深理解6軸陀螺儀姿態解算算法(下)
?
==================================================================
????????花了近一個星期的每個晚上,試圖將6軸陀螺儀姿態解算算法的每一步前因后果講清楚,有概念引用,也有公式推導,約2萬字,實屬不易,轉載請注明出處,看了感覺對您有幫助的,勞煩點個贊,謝謝!
? ? ? ? 對于我們工作實踐中的很多算法,能用不等于會用, 從扎實的理論基礎開始,完全掌握它,并能做到根據實際的問題需求去修改調整它,才能把問題解決的更好.
? ? ? ? 好了, Enjoy it.
==================================================================
? ? ? ? 多年前,工作中就曾用到Mahony的6軸陀螺儀姿態解算算法(以下簡稱算法),用我當時初看這個算法的的感悟講就是:"這算法一行一行都能看明白,但兩行或多行放一起就蒙圈了."? 記得后來把算法背后的知識點弄明白,才敢說,這個算法我看懂了.
? ? ? ? 這個算法想講明白其實并不容易,因為背后的知識點太多,每個細節都講明白了就夠寫幾個章節了. 特別是自下而上,嘗試把各個知識點堆積起來,來講解這個算法,那就得長篇連載.
? ? ? ? 我試圖通過另一種方式來講解這個算法: 即采用自上而下為主,自下而上為輔 相結合的方式,來講解這個算法. 大致過程就是: 先講解算法依賴的一些最基本的概念,然后在此基礎上從整體上理解算法的基本邏輯,最后針對算法中關鍵的幾個知識點,自上而下挖掘其理論基礎;
本文基本目錄結構如下:
<上篇>:
一. 算法依賴的最基本概念?
? ? ? ? 1. 載體坐標系
? ? ? ? 2. 地理坐標系
? ? ? ? 3. 歐拉角
? ? ? ? 4. 四元數
????????5. 常見旋轉表示法
二. 算法基本思想
三. 算法源碼及居高臨下看算法流程框圖
<中篇>:
四. 方向余弦矩陣, 歐拉旋轉,四元數旋轉 等理論基礎??
<下篇>:
五.對算法中關鍵知識點進行重點講解? ?
? ? ? ? 1.?關鍵知識點1:?當前姿態四元數q(參考坐標n系)算出重力在三個軸上的分量(載體坐標b系)
? ? ? ? 2.?關鍵知識點2:?用兩個向量叉積(也叫向量積,外積),來表示載體坐標系角速度分量誤差error
? ? ? ? 3.?關鍵知識點3:?四元數微分方程,一階畢卡解法,融合修正后陀螺儀姿態到當前四元數q中
? ? ? ? 4.?關鍵知識點4:?把用四元數q表示的姿態轉化為用歐拉角表示的姿態
----------------------------------------正文開始--------------------------------------
一. 算法依賴的最基本概念
1. 載體坐標系
????????載體坐標系是依附在物體本身上雖物體一起運動的本地坐標系,類似人體理解的上下左右前后.一般陸地車輛的載體坐標系如下圖所示,原點
固定在物體的重心,
沿載體橫向指向載體的右側,
沿載體縱向指向載體的前方,
沿載體的豎軸指向載體的上方.?
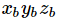三軸的構成的坐標系符合右手直角坐標系法則.(飛行器的載體坐標系一般為前向,這里僅討論四輪車,具體以實際陀螺儀芯片安裝方位為準,算法也要相應做調整)
? ? ? ? 車載6軸陀螺儀的角速度輸出和加速度計加速度輸出,都是針對載體坐標系的.
2. 地理坐標系OENξ
????????如下圖所示,地理坐標系OENξ的原點O取在載體的重心,E軸指向當地地理方向:東方,N軸指向當地地理方向: 北方,ξ軸沿當地地垂線指向:上方.?OENξ三軸的構成的坐標系符合右手直角坐標系法則. 地理坐標系跟隨載體運動,但三軸指向不會變化. 類似人體理解的相對自身位置的前后左右上下為載體坐標系,但描述方位的東西南北天地為地理坐標系,你在地球上(僅限地球上)走到哪里地理坐標原點都跟到哪里,但方位始終不變.
? ? ? ? 一般情況下,對陸地四輪車而言,地理坐標系OENξ就是導航坐標系. 對于沒有加裝磁力計的載體,無法準確識別出真實的地理方位,其地理坐標系一般以初始狀態為準.
? ? ? ? 算法的目的就是: 將針對載體坐標系的角速度和加速度數據,按照一定的算法變換到地理坐標系OENξ, 最終解算出載體在地理坐標系下的用歐拉角表示的姿態: 偏航角(yaw),俯仰角(pitch),翻滾角(roll).
????????NOTE:?俯仰角(pitch)和翻滾角(roll),具體哪個是相對于x軸旋轉,哪個是相對于y軸旋轉,請以實際陀螺儀芯片安裝方位為準,算法也要相應做調整.
3. 歐拉角(這里先僅引入概念)
? ? ? ? 以四輪車而言, 歐拉旋轉就是物體以一定順序分別繞載體坐標系三個坐標軸(x,y,z軸）旋轉一定的角度。這個分別相對于三軸的旋轉角度就是歐拉角.?一般沿載體前后縱向軸旋轉稱翻滾(roll),沿載體橫向軸旋轉稱俯仰(pitch),沿載體上下垂線旋轉稱偏航(yaw), 旋轉完成后載體相對于導航坐標系(地理坐標系)的姿態用歐拉角表示為翻滾角(roll),俯仰角(pitch),偏航角(yaw). 歐拉角是一系列坐標軸旋轉順序的組合.? 即它與x,y,z三軸旋轉順序密切相關. 交換順序就是不同的旋轉.
? ? ? ? 歐拉旋轉可以是以載體坐標系表示,也可以以導航坐標系表示. 如下圖:? 做圖中繞載體坐標系的三次繞軸旋轉后,求載體相對于地理坐標系的姿態的歐拉角表示(這里僅引出概念,并不求解).
Note:? 注意歐拉旋轉和歐拉角的不同和關系: 歐拉旋轉是給定三個角度(三軸旋轉角度),然后按一定的順序先后繞三軸旋轉指定的角度(這里的軸一般是載體坐標系三軸),其是一個過程. 歐拉角一般指載體靜態狀態,或一個歐拉旋轉完成后,載體坐標系相對于導航坐標系的翻滾角(roll),俯仰角(pitch),偏航角(yaw),其是一個狀態值.
???????? 在慣性導航系統中,我們更關心目標載體在任意時刻,載體坐標系和導航坐標系(地利坐標系OENξ)三軸之間的角度關系,即坐標旋轉變換.?? Note:這里的兩個坐標系三軸之間的角度關系不同于歐拉角(roll,pitch,yaw).? 但通過兩個坐標系三軸之間的關系,可以求出載體在導航坐標下的姿態,用歐拉角(roll,pitch,yaw)表示.
4. 四元數(這里先僅引入概念)
? ? ? ? 我們中學學過復數, 形如 z=a+bi（a、b均為實數）的數稱為復數。其中，a 稱為實部，b 稱為虛部，i 稱為虛數單位。四元數是復數基礎上的擴展, 是由實數加上三個虛數單位 i、j和k 組成，四元數一般可表示為z=a + bi+ cj + dk，其中a、b、c 、d是實數,?i2 = j2 = k2 = -1， io = jo = ko = 1?。對于i、j和k本身的幾何意義可以理解為一種旋轉，其中i旋轉代表Z軸與Y軸相交平面中Z軸正向向Y軸正向的旋轉，j旋轉代表X軸與Z軸相交平面中X軸正向向Z軸正向的旋轉，k旋轉代表Y軸與X軸相交平面中Y軸正向向X軸正向的旋轉，-i、-j、-k分別代表i、j、k旋轉的反向旋轉。
? ? ? ? 三維坐標系下空間的一個點P(x,y,z),用四元數表示就是p = (0,x,y,z),也有矢量表示法p = (P(x,y,z), 0)或p = (0,P(x,y,z)).
?5. 常見旋轉表示法
* 旋轉矩陣(更多細節,自行學習,比如3D數學基礎)
????????旋轉矩陣是在用旋轉矩陣乘以(不同平臺有左乘和右乘之分)一個向量,其結果改變向量的方向但不改變大小的效果.矩陣旋轉使用了一個4*4大小的矩陣來表示繞任意軸旋轉的變換矩陣.
在計算時，我們將當前向量右乘R.? 即:? p’ = pR
*歐拉旋轉(更多細節,自行學習)
????????一般是先繞X軸旋轉α角度,再繞Y軸旋轉β角度,最后繞Z軸旋轉γ角度. 即 一次只旋轉一個分量,按順序累積.?? 其旋轉矩陣為:
R =?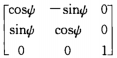
=?
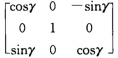
?在計算時，我們將當前坐標,當做列向量右乘R.? 即:? p’ = pR
*四元數旋轉(更多細節,自行學習)
?????????假定某矢量繞通過O點的某軸逆時針轉動一個角度θ，則與該矢量固連的動坐標系和參考坐標系間的變換四元數為：q=cos(θ/2)+sin(θ/2)cosα?i+ sin(θ/2)cosβj+ sin(θ/2)cosγ?k,通常稱其為四元數的三角形式，也稱特征四元數，其范數為1，在導航應用中一般所應用的四元數均為特征四元數。其標量部分cos(θ/2)表示了轉角一半的余弦值，矢量部分則體現了轉動軸的方向，α、β、γ是轉動軸與參考坐標系各軸間的夾角。
????????旋轉矢量坐標變換的四元數描述為：p′=qpq?1? ?根據四元數相關特性有:?p’=qpq*, 反過來有: p=q*p’q
*這么多描述旋轉的方法,為什么算法使用四元數?
| 旋轉描述法 | 優點 | 缺點 |
| 矩陣旋轉 | 旋轉軸可以是任意向量 | 旋轉其實只需要知道一個向量+一個角度，一共4個值的信息，但矩陣法卻使用了16個元素； 矩陣乘法操作時計算量大，造成了空間和時間上的一些浪費； |
| 歐拉旋轉 | 很容易理解，形象直觀； | 要按照一個固定的坐標軸的順序旋轉的，因此不同的順序會造成不同的結果； 會造成萬向節鎖（Gimbal Lock）的現象; 由于萬向節鎖的存在，歐拉旋轉無法實現球面平滑插值. |
| 四元數旋轉 | 可以避免萬向節鎖現象； 只需要一個4維的四元數就可以執行繞任意過原點的向量的旋轉，方便快捷，在某些實現下比旋轉矩陣效率更高； 可以提供平滑插值； | 比歐拉旋轉稍微復雜了一點點，因為多了一個維度； 理解更困難，不直觀. |
? ? ? ? 熟悉Unity3D開發的朋友應該熟悉,Unity3D為了更直觀的展示旋轉,在界面上展示的是歐拉角旋轉,而起內部實現的卻是四元數旋轉(避免萬向節鎖).
? ? ? ? 對于很多嵌入式設備而言, CPU資源很寶貴,又因為6軸陀螺儀姿態解算算法調用周期一般都是毫秒級,相當頻繁. 顯然使用四元數表示旋轉更合適.?
????????本算法也一樣,? 為了計算高效同時避免萬向節鎖問題, 坐標旋轉變換使用四元數, 姿態融合使用歐拉角, 最終姿態輸出也使用歐拉角.
? ? ? ? 當然現在很多陀螺儀芯片(比如: MPU-6050),都已經芯片內置(SoC)姿態解算算法,直接通過IIC使用命令獲取即可.
二. 算法基本思路
????????理論上,加速度計和陀螺儀的輸出都可以單獨用來計算姿態, 為什么還要進行姿態融合呢? 正如前幾篇我發表的關于卡爾曼濾波器的文章,任何測量值都有噪音存在誤差,同時預測也有誤差,需要使用多方數據進行融合,獲得最優估計.
????????這里加速度計的測量值對系統震動相當敏感,數據波動較大,短期可信度低,但經濾波后數據長期來看可信度高; 而陀螺儀對系統震動不敏感短期可信度高,但陀螺儀存在漂移會累加,所以長期來看可信度低.? 所以可以利用算法短期相信陀螺儀,長期相信加速度計,對兩者進行姿態融合. (記得真正的算法開始之前,對陀螺儀和加速度計的原始數據進行單位換算, 靜態校準,數據濾波等初始化工作).
如下圖,載體水平靜止時, 加速度計的三軸和陀螺儀的三軸分別在載體坐標系下的方向和分量大小(向量長度僅是演示).
????????但當載體處于任意其他狀態時, 比如運動或傾斜時,?加速度計的三軸和陀螺儀的三軸分別在載體坐標系下的方向不變,但分量大小發生改變(向量長度僅是演示).如下圖:
????????但, 這里的各分量表示的姿態都是基于載體坐標系的,我們需要的是基于導航坐標系(地理坐標系OENξ)的姿態.
?本算法的基本思路如下:
1. 用一個全局的四元數q(q0 , q1,??q2 , q3 )表示載體在地理坐標系OENξ下的姿態,其中初始值q0 = 1, q1 = 0, q2 = 0, q3 = 0,每個計算周期都將計算出的地理坐標系OENξ下的姿態結果歸一化后保存在該四元數q中;
2.根據余弦矩陣,歐拉角和四元數旋轉表示法(這是關鍵點(1)放最后講),把當前地理坐標系OENξ下的四元數q姿態轉換為載體坐標系下的加速度計的三個分量ax`,ay`,az`(為單位向量);
3.對當前加速度計測量值ax,ay,az歸一化為單位向量, 利用兩個單位向量的叉乘,衡量兩個向量的偏差(這是關鍵點(2)放最后講), 計算出三軸分量的偏差: error_x,error_y,error_z;
4.對各個計算周期的三分量偏差做累加積分:?xErrorIntegral,yErrorIntegral ,yErrorIntegral ;
5.因為加速度計數據長期累積可信度大,而陀螺儀短期測量值可信度大,所以把加速度計的本次偏差和累積積分對陀螺儀的測量值gx,gy,gz做修正,? 補償陀螺儀的零點漂移.使本次測量值gx,gy,gz更準確;
6.利用四元數微分方程. 采用一階畢卡解法(這是關鍵點(3)放最后講)，融合修正過的陀螺儀測量值gx,gy,gz到位于地理坐標系OENξ下的當前姿態四元數q.
7.對更新后的地理坐標系OENξ下的姿態四元數q進行歸一化(單位化),單位化四元數在空間旋轉時不會拉伸，僅有旋轉角度;
8.利用余弦矩陣,四元數旋轉到歐拉角的轉換(這是關鍵點(4)放最后講)，求出地理坐標系OENξ下四元數q,對應的更形象更直觀的歐拉角姿態表示:?翻滾角(roll),俯仰角(pitch),偏航角(yaw).
9.最新的地理坐標系OENξ下載體的姿態扔保存在四元數q中,供下個周期計算使用;
Note:? 發現這個基本思路寫太過了,過于詳細,回頭再改改.
三. 算法源碼及居高臨下看算法流程框圖
? ? ? ? 為了調試時翻轉方便,我是在android手機上跑的Mahony的6軸陀螺儀姿態解算算法源碼,android手機上陀螺儀坐標軸都是手機從左側到右側的水平方向為x軸正向，從手機下部到上部為y軸正向，垂直于手機屏幕向上為z軸正向,這與陸地四輪車載體坐標系表示法一致. 此源碼來自網上,我只是針對手機的載體坐標系做了調整,加速度計(m/s)和陀螺儀(rad/s)數據都是用的android系統API獲取的原始數據,沒做任何加工.源碼如下:
#define sampleFreq 100.f // sample frequency in Hz/*采樣周期的一半，用于求解四元數微分方程時計算角增量請確定自己的姿態調用周期: 10ms,即上面的sampleFreq: 100Hz*/#define halfT 0.005f//這里的Kp,Ki是用于控制加速度計修正陀螺儀積分姿態的速度#define Kp 10.0f //2.0f#define Ki 0.008f //0.002f//初始姿態四元數(地理坐標系)，q(q0,q1,q2,q3)static float q0 = 1, q1 = 0, q2 = 0, q3 = 0; //最優估計四元數//定義姿態解算誤差的積分. //當前加計測得的重力加速度在三軸(x,y,z)上的分量,與當前姿態計算得來的重力在三軸上的分量的誤差的積分static float xErrorInt = 0, yErrorInt = 0, zErrorInt = 0;/* * 6軸陀螺儀姿態融合算法: Mahony的互補濾波算法 6軸版 * 單位: m/s^2 rad/s * 由于加速度的噪音很大, 此處建議使用濾波后的數據 * */void MahonyImuUpdate(float gx, float gy, float gz, float ax, float ay, float az, IMU_Angle* angle)//g表陀螺儀，a表加計{ float q0temp,q1temp,q2temp,q3temp;//四元數暫存變量，求解"微分方程"時要用 float norm; //矢量的模或四元數的范數 float posture_x, posture_y, posture_z;//當前姿態計算得來的重力在三軸上的分量 //當前加計測得的重力加速度在三軸上的分量,與用當前姿態計算得來的重力在三軸上的分量的誤差 float error_x, error_y, error_z; // 先把這些用得到的值算好 float q0q0 = q0*q0, q0q1 = q0*q1, q0q2 = q0*q2, q0q3 = q0*q3, q1q1 = q1*q1, q1q2 = q1*q2; float q1q3 = q1*q3, q2q2 = q2*q2, q2q3 = q2*q3, q3q3 = q3*q3; //加計處于自由落體狀態時不進行姿態解算，因為會產生分母無窮大的情況 if( (ax == 0.0f) && (ay == 0.0f) && (az == 0.0f) ) return; //將加速度的原始數據進行歸一化,得到單位加速度 norm = sqrt(ax*ax + ay*ay + az*az);//單位化加速度計， ax = ax / norm; ay = ay / norm; az = az / norm; //用當前姿態(參考坐標n系)計算出重力在三個軸上的分量(載體坐標b系)， /*把四元數換算成"方向余弦矩陣"中的第三列的三個元素.根據余弦矩陣和歐拉角的定義,地理坐標系的重力向量,轉到載體坐標系,正好是這三個元素.*/ posture_x = 2*(q1q3 - q0q2); posture_y = 2*(q0q1 + q2q3); posture_z = q0q0 - q1q1 - q2q2 + q3q3; //計算: 傳感器測得的重力與當前姿態計算的重力間的誤差，向量外積可以表示這一誤差 // Error is sum of cross product between estimated and measured direction of gravity error_x = (ay*posture_z - az*posture_y) ; error_y = (az*posture_x - ax*posture_z) ; error_z = (ax*posture_y - ay*posture_x) ; //對兩種重力分量的叉積誤差進行積分 xErrorInt = xErrorInt + error_x * Ki;// * (1.0f / sampleFreq); yErrorInt = yErrorInt + error_y * Ki;// * (1.0f / sampleFreq); zErrorInt = zErrorInt + error_z * Ki;// * (1.0f / sampleFreq); //對兩種重力分量的叉積誤差的積分做p,i修正陀螺零偏,通過調節Kp,Ki兩個參數,可以控制加速度計修正陀螺儀積分姿態的速度 gx = gx + Kp*error_x + xErrorInt; //將誤差PI后補償到陀螺儀，即補償零點漂移 gy = gy + Kp*error_y + yErrorInt; gz = gz + Kp*error_z + zErrorInt; //這里的gz由于沒有觀測者進行矯正會產生漂移，表現出來的就是積分自增或自減 // Integrate rate of change of quaternion //gx *= (1.0f / sampleFreq); // pre-multiply common factors //gy *= (1.0f / sampleFreq); //gz *= (1.0f / sampleFreq); //下面進行姿態的更新，也就是四元數微分方程的求解 q0temp=q0;//暫存當前值用于計算 q1temp=q1; q2temp=q2; q3temp=q3; //四元數微分方程. 采用一階畢卡解法，融合當前位姿和陀螺儀測量值,并轉換到世界參考坐標系N. q0 = q0temp + (-q1temp*gx - q2temp*gy -q3temp*gz)*halfT; q1 = q1temp + (q0temp*gx + q2temp*gz -q3temp*gy)*halfT; q2 = q2temp + (q0temp*gy - q1temp*gz +q3temp*gx)*halfT; q3 = q3temp + (q0temp*gz + q1temp*gy -q2temp*gx)*halfT; //對當前姿態四元數進行單位化,單位化四元數在空間旋轉時不會拉伸，僅有旋轉角度 norm = sqrt(q0q0 + q1q1 + q2q2 + q3q3); q0 = q0 / norm; q1 = q1 / norm; q2 = q2 / norm; q3 = q3 / norm; //再次把這些用得到的值算好 q0q1 = q0*q1; q0q2 = q0*q2; q0q3 = q0*q3; q1q1 = q1*q1; q1q2 = q1*q2; q1q3 = q1*q3; q2q2 = q2*q2; q2q3 = q2*q3; q3q3 = q3*q3; //四元數到歐拉角的轉換,這里輸出的是弧度,想要角度值,可以直接乘以57.3,即一弧度對應角度值 angle->roll = atan2f(2.f * (q0q1 + q2q3),1 - 2.f * ( q1q1 - q2q2) ); // roll: X軸 angle->pitch = asinf(2.f * (q0q2 - q1q3) ); // pitch: Y軸 //其中YAW航向角由于加速度計對其沒有修正作用，因此實際結果會逐漸偏移,想要準確,需要使用磁力計 angle->yaw = atan2f(2.f * (q0q3 + q1q2),1 - 2.f * (q2q2 + q3q3) ); // yaw: Z軸/* Note: 上面轉歐拉角的代碼,其實有個問題,就是該代碼是針對飛行器導航設計的,其前后縱向軸為載體坐標系Oxyz的x軸,而不是陸地四輪車那樣前后縱向軸為載體坐標系Oxyz的y軸.但不要擔心, 學習了本文后,你也可以動手修改它.*/}????????Note: 上面的代碼,其實有個問題,就是該代碼是針對飛行器導航設計的,其前后縱向軸為載體坐標系Oxyz的x軸,而不是陸地四輪車那樣前后縱向軸為載體坐標系Oxyz的y軸.但不要擔心, 學習了本文后,你也可以動手修改它.
下面站一定高度來觀察算法流程框圖,然后在對算法中4個關鍵知識點,逐一攻克:
四.方向余弦矩陣, 歐拉旋轉,四元數旋轉 理論基礎?(見中編)
?????十三.四輪車驅動開發之五: 由淺至深理解6軸陀螺儀姿態解算算法(中)???